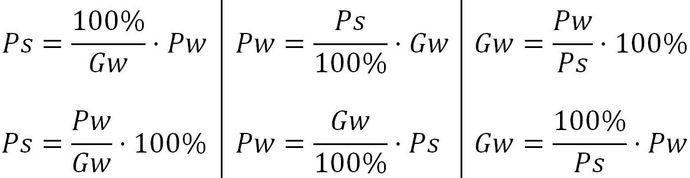Prozentrechnen: Formeln zur Prozentrechnung

Im Privatleben wie im Beruf, stehen Menschen ständig vor der Aufgabe, Prozente ausrechnen und vergleichen zu müssen. Im Privatleben können das Preisnachlässe in Geschäften sein, Zinsen berechnen für Kapitalanlage, Ratenzahlungen bei Kreditverträgen und viele Dinge mehr. Im Berufsleben kommt das Prozentrechnen eigentlich in jeder Branche und in fast jedem Beruf vor.

Im kaufmännischen Bereich gehört z.B. die Berechnung der Mehrwertsteuer, die Aushandlung von Rabatten beim Einkauf und Verkauf, die Berechnung von Provisionen, die Auswertung statistischer Daten wie Zuwachs der Bestellungen etc. zum Alltag. Aber auch im fertigungstechnischen Bereich wird die Prozentrechnung häufig angewendet, z.B. für Berechnungen über den optimalen Materialeinsatz, über Auslastung der Maschinenzeiten, Kontrolle über die Reduzierung des Verschnitts und einiges mehr. Daher gehören Kenntnisse über die Prozentrechnung zu den Grundlagen, die jeder Mitarbeiter beherrschen sollte.

Formelzeichen und Formeln zum Prozentrechnen

In Formeln zur Prozentrechnung werden üblicherweise folgende Formelzeichen und Zahlen benutzt:

Prozentsatz: Formelzeichen Ps
Grundwert: Formelzeichen Gw
Prozentwert: Formelzeichen Pw
100%

Nachfolgend die Formeln für den Grundwert, den Prozentsatz und den Prozentwert sowie die Erläuterung über die Grundlagen zum Prozentrechnen und den Formeln in Bildergalerien.

Grundlagen der Prozentrechnung

1. Die Prozentrechnung dient zur Berechnung von Anteilen. Hierzu ein Beispiel. Man stelle sich vor, man hat 3 Getränkedosen zwischen Person A und Person B zu verteilen.
2. Person A bekommt 2 Dosen, Person B bekommt 1 Dose.
3. Umgangssprachlich würde man dazu 2 Drittel und 1 Drittel sagen.
4. Die Werte 2 Drittel und 1 Drittel kann man als Bruch darstellen und bei kleinen Mengen behält man den Überblick.
5. Je größer die Mengen werden, umso mehr verliert man jedoch den Überblick. Man muss sich das z.B. vorstellen, wenn man 329 Dosen zwischen 14 Personen aufteilen würde. Da hilft auch die Darstellung als Bruch wenig.
6. Die Lösung für das Problem ist die Angabe in Prozent.
7. Dabei wird der Grundwert (die gesamte Menge), in diesem Fall 11 Stück, als 100% betrachtet.
8. Teilt man jetzt die Mengen auf, ist die Darstellung der Anteile viel übersichtlicher. In diesem Beispiel erhält Person A 64% (gerundet). Diesen Wert nennt man Prozentsatz. Das würde fast 2 Drittel entsprechen und ist wesentlich anschaulicher als 7 Elftel.
9. Der Prozentwert entspricht der tatsächlichen Menge, die der Prozentsatz ausmacht. Das bedeutet, 64% von 11 Getränkedosen sind 7 Dosen. Beim Prozentrechnen geht es vorwiegend darum, Grundwert, Prozentwert und Prozentsatz auszurechnen.

Ermitteln des Prozentsatzes

1. Ziel ist, einen Weg zu finden, um den Prozentsatz zu ermitteln.
2. Wie viel Prozent entspricht eine Menge, die man vom Grundwert entnimmt?
3. Zuerst teilt man 100% durch die Grundmenge. So ermittelt man den Prozentsatz für 1 Einheit.
4. Zur besseren Veranschaulichung kann man sich das wie eine Gleichung vorstellen.
5. Nachdem der Prozentsatz für 1 Einheit ermittelt wurde, braucht man diesen nur noch mit dem Prozentwert zu multiplizieren.
6. Der Rechenweg ist also: 100% durch den Grundwert teilen, danach mit dem Prozentwert multiplizieren.
7. Die Formel für den Prozentsatz (Ps): 100 : Gw · Pw oder Pw : Gw · 100%.

Ermitteln des Prozentwerts

1. Das Ziel ist diesmal, den Prozentwert von 64% zu ermitteln.
2. Wie viel Stück entsprechen 64% vom Grundwert?
3. Man teilt den Grundwert durch 100%, so erhält man die Stückzahl für 1%.
4. Zur besseren Veranschaulichung kann man sich das wie eine Gleichung vorstellen.
5. Nachdem die Stückzahl für 1% ermittelt wurde, braucht man diesen nur noch mit dem Prozentsatz zu multiplizieren.
6. Der Rechenweg ist: Teile den Grundwert durch 100%, danach multipliziere mit dem Prozentsatz.
7. Die Formel für den Prozentwert (Pw): Gw : 100 · Ps oder Ps : 100 · Gw.

Ermitteln des Grundwerts

1. Das Ziel ist diesmal, den Grundwert zu ermitteln.
2. Wie viel Stück entsprechen 100% vom Grundwert?
3. Man teilt den Prozentwert durch den Prozentsatz, so erhält man die Stückzahl für 1%.
4. Zur besseren Veranschaulichung kann man sich das wie eine Gleichung vorstellen.
5. Nachdem die Stückzahl für 1% ermittelt wurde, bruacht man diesen nur noch mit 100% zu multiplizieren.
6. Der Rechenweg ist: Teile den Prozentwert durch den Prozentsatz, danach multipliziere mit 100%.
7. Die Formel für den Prozentwert (Gw): Pw : Ps · 100 oder 100 : Ps · Pw.