Dreieck berechnen
Ein Dreieck ist eine geometrische Form mit 3 Punkten, 3 Winkeln und 3 Seiten. Die Punkte werden häufig in Großbuchstaben A, B und C benannt. In Kleinbuchstaben benennt man die jeweils zum Punkt gegenüberliegende Seite, also a, b und c. Die Winkel werden als α (Punkt A), β (Punkt B) und γ (Punkt C) benannt. Alle 3 Winkel ergeben zusammen immer 180°. Ist der Winkel γ größer als 90°, sind die beiden anderen Winkel zwangsläufig spitz.
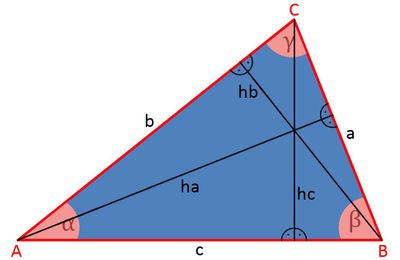
Rechtwinklige Dreiecke können z.B. mit dem Satz des Pythagoras oder mit den Winkelfunktionen berechnet werden. Hat man es nicht mit einem rechtwinkligen Dreieck zu tun, so stellt das trotzdem kein Problem dar. Denn, jedes Dreieck kann durch die Ziehung der Höhenlinien ha (Höhe zu a), hb (Höhe zu b) und hc (Höhe zu c) in rechtwinklige Dreiecke zerlegt werden. Dabei werden die Seiten a, b und c geteilt.
Ermitteln des Sinussatzes
Auf der Seite Trigonometrie im Einheitskreis wird erläutert, wie die Winkelfunktionen für rechtwinklige Dreiecke sind. Wenn man davon ausgeht, dass die Teilstrecken von a, b und c nicht bekannt sind, kann man diese trotzdem berechnen, wenn man folgende Winkelfunktion nimmt:
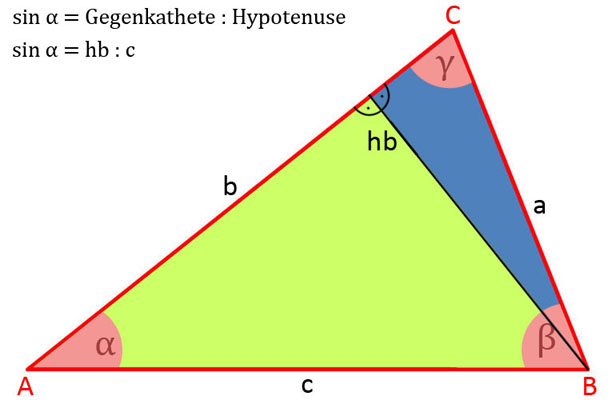
- sin α = Gegenkathete : Hypotenuse
Diese Funktion kann auf die rechtwinkligen Teildreiecke angewendet werden. Wichtig ist dabei nur, dass man genau weiß, was bei den Teildreiecken die Ankathete, Gegenkathete und Hypotenuse ist. Als Ergebnis erhält man folgende Gleichungen:
- sin α = hb : c
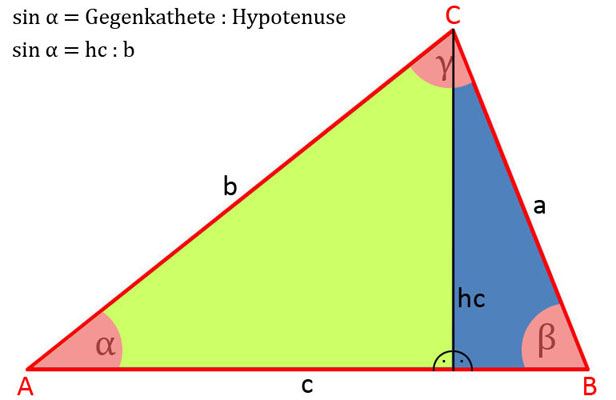
- sin α = hc : b
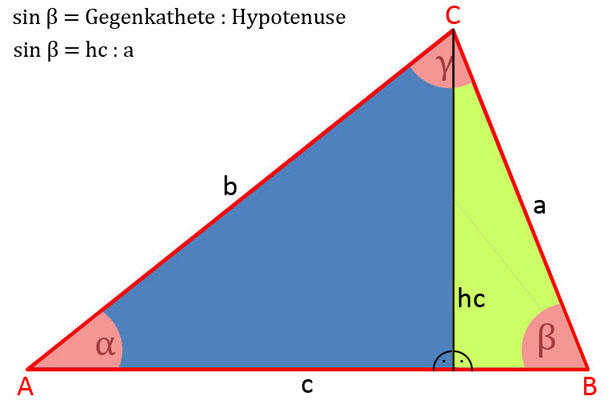
- sin β = hc : a
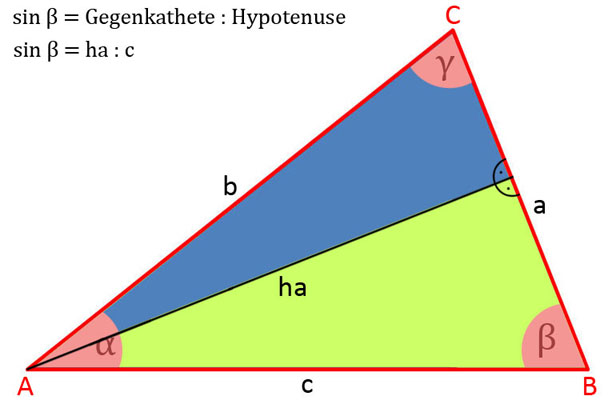
- sin β = ha : c
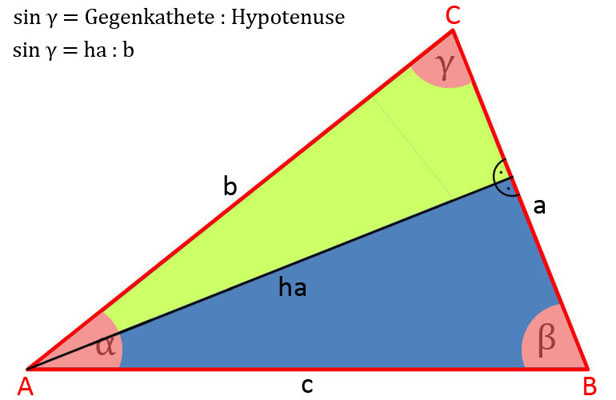
- sin γ = ha : b
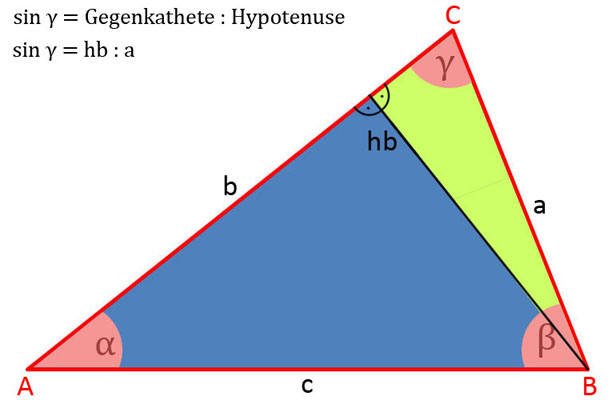
- sin γ = hb : a
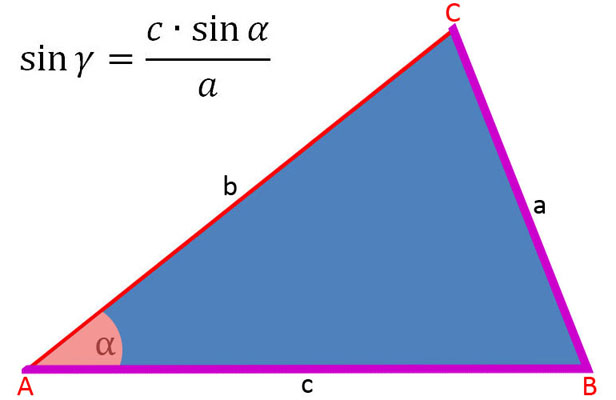
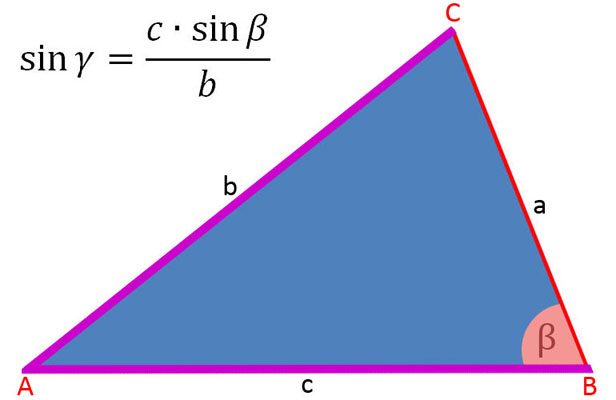
Nachfolgend die Erläuterung in der Bildergalerie, wann man die Seiten a, b und c, die Höhen ha, hb und hc als Ankathete, Gegenkathete und Hypotenuse in die Funktion sin α = Gegenkathete : Hypotenuse einsetzt und die Gleichungen bildet.
Im nächsten Schritt stellt man die Formeln um, so dass man die Höhen ha, hb und hc berechnen kann:
- ha = c · sin β
- ha = b · sin γ
- hb = a · sin γ
- hb = c · sin α
- hc = b · sin α
- hc = a · sin β
Da man mit jeweils zwei Gleichungen die Höhen ha, hb und hc ermitteln kann, kann man wieder neue Gleichungen bilden:
- c · sin β = b · sin γ
- a · sin γ = c · sin α
- b · sin α = a · sin β
Im nächsten Schritt kann man wieder die Gleichungen umstellen, um dann folgende Formeln zu erhalten:
- sin α = a · sin γ : c
- sin β = b · sin α : a
- sin γ = c · sin β : b
Die Gleichungen werden erneut umgestellt und man erhält folgenden interessanten Gleichungssatz, der Sinussatz genannt wird:
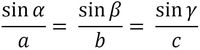
Ein erneutes Umstellen durch Kehrwert der Quotienten ergibt folgenden Sinussatz:
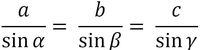
Formt man das erneut um, erhält man folgenden Sinussatz:
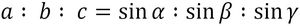
Voraussetzungen, um ein Dreieck eindeutig zu konstruieren
Aus all den Gleichungen lässt sich ablesen, dass man mit dem Sinussatz ein Dreieck berechnen und exakt konstruieren kann, wenn man eine der folgenden Informationen hat:
- Zwei Winkel und eine Seite, hierbei hat man natürlich automatisch den dritten Winkel, da die Winkelsumme 180° ist
- Zwei Seiten und ein Winkel, wobei der Winkel nicht von den beiden Seiten eingeschlossen sein darf
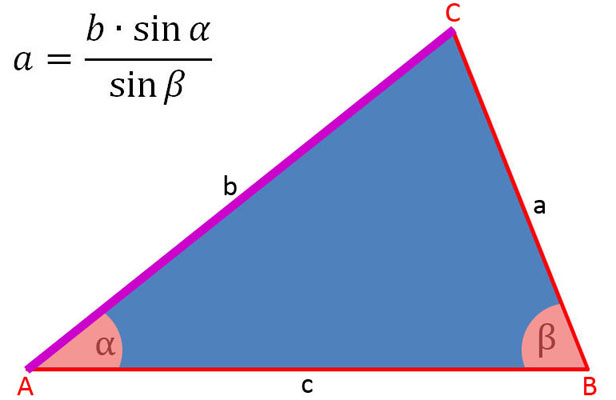
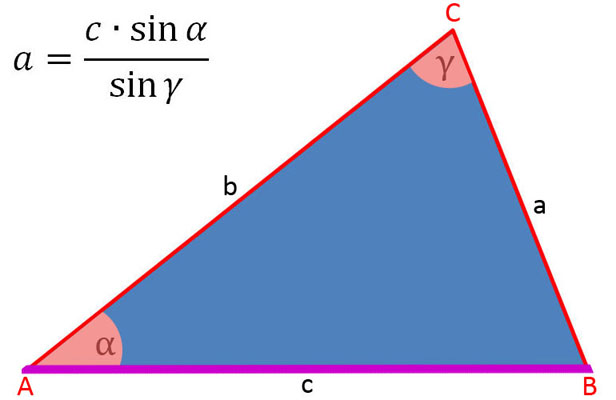
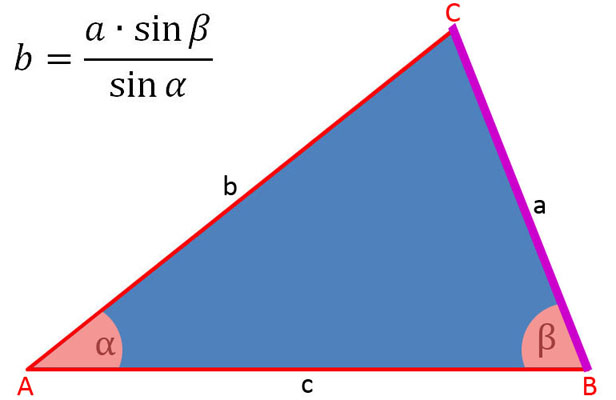
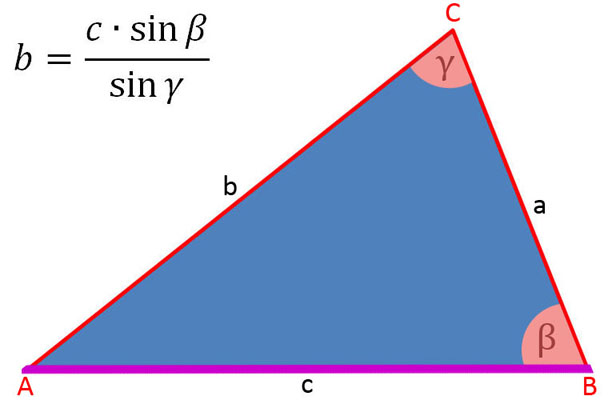
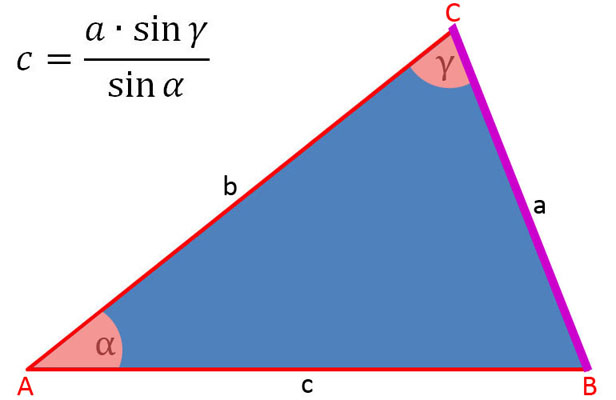
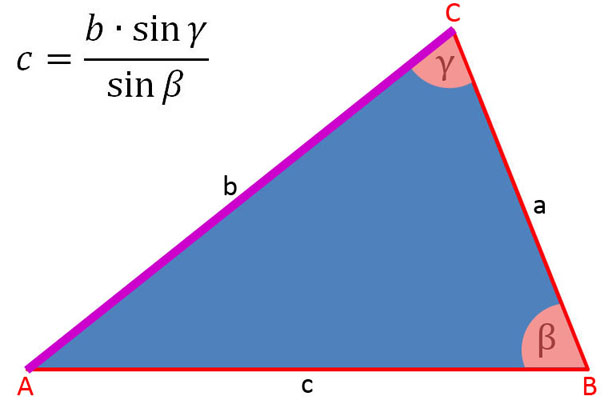
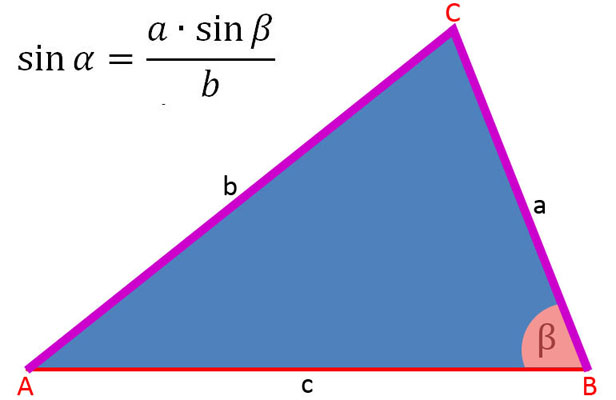
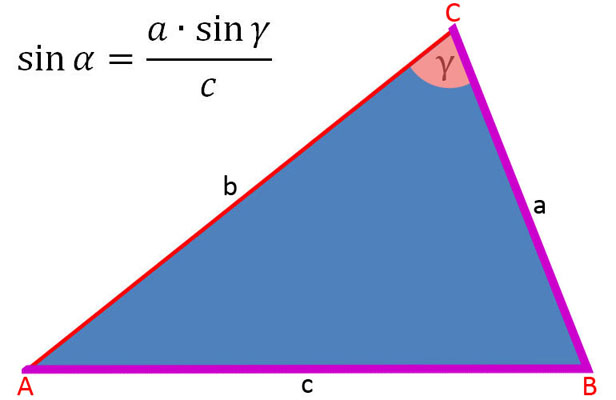
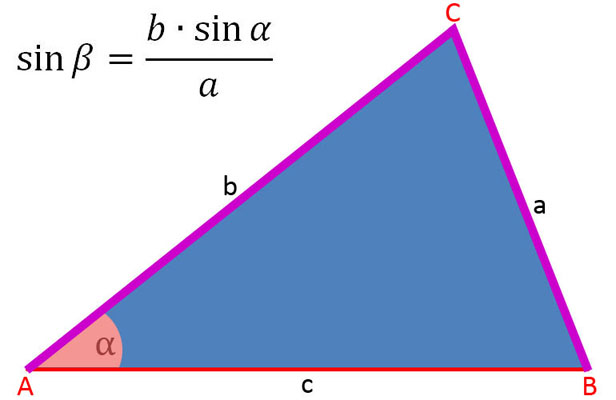
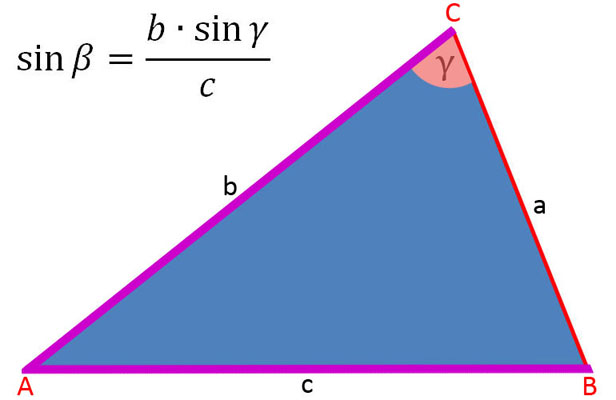
In der folgenden Bildergalerie sind die Sinussätze soweit umgestellt, um die Seiten a, b und c sowie sin α, sin β und sin γ zu berechnen.
Dreiecke, die nicht mit dem Sinussatz berechnet werden können
Mit dem Sinussatz kann man bereits viele Dreiecke berechnen. Es gibt jedoch zwei Situationen, in den man den Sinussatz nicht anwenden kann.
- Zwei Seiten und ein Winkel sind bekannt, jedoch ist der bekannte Winkel eingeschlossen
- Alle drei Seiten sind bekannt, jedoch kein Winkel
Bei der ersten Situation muss man zunächst die unbekannte Seite ermitteln, sind alle 3 Seiten, jedoch kein Winkel bekannt, braucht man den Wert eines unbekannten Winkels. Hierfür kann der Kosinussatz angewendet werden. Hat man den Wert der unbekannten Seite bzw. vom unbekannten Winkels ermittelt, kann man danach mit den Sinussätzen die übrigen fehlenden Werte ermitteln.