Verlauf der Winkelfunktionen

Auf der Seite Trigonometrie im Einheitskreis wird erläutert, wie das Verhältnis der Seiten Ankathete, Gegenkathete und Hypotenuse im Zusammanhang mit dem Winkel α zueinander stehen. Der Verlauf von Sinus, Kosinus oder Tangens kann grafisch abgebildet werden, Sie werden in den folgenden Bildergalerien dargestellt.

Sinus (sin α)

1. Bei α = 0° ist auch sin α = 0.
2. Bei α = 30° ist sin α = 0,5.
3. Bei α = 60° ist sin α = 0,866.
4. Bei α = 90° ist sin α = 1.
5. Bei α = 120° ist sin α = 0,866.
6. Bei α = 150° ist sin α = 0,5.
7. Bei α = 180° ist sin α = 0.
8. Bei α = 210° ist sin α = -0,5 und somit im negativen Bereich.
9. Bei α = 240° ist sin α = -0,866.
10. Bei α = 270° ist sin α = -1.
11. Bei α = 300° ist sin α = -0,866.
12. Bei α = 330° ist sin α = -0,5.
13. Bei α = 360° ist sin α wieder wie bei 0° und somit 0.
14. Der Verlauf der Sinuskurve.
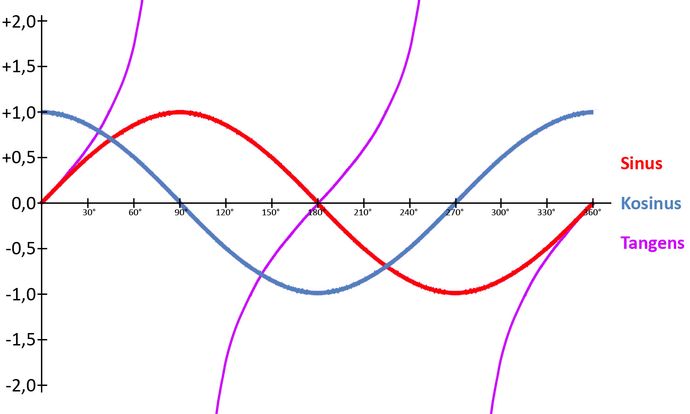
15. Übersicht der Verläufe von Sinus, Kosinus und Tanges.

Kosinus (cos α)

1. Bei α = 0° ist auch cos α = 1.
2. Bei α = 30° ist cos α = 0,866.
3. Bei α = 60° ist cos α = 0,5.
4. Bei α = 90° ist cos α = 0.
5. Bei α = 120° ist cos α = -0,5 und somit im negativen Bereich.
6. Bei α = 150° ist cos α = -0,866.
7. Bei α = 180° ist cos α = -1.
8. Bei α = 210° ist cos α = -0,866.
9. Bei α = 240° ist cos α = -0,5.
10. Bei α = 270° ist cos α = 0.
11. Bei α = 300° ist cos α = 0,5.
12. Bei α = 330° ist cos α = 0,866.
13. Bei α = 360° ist cos α wieder wie bei 0° und somit 1.
14. Der Verlauf der Kosinuskurve.
15. Übersicht der Verläufe von Sinus, Kosinus und Tanges.

Tangens (tan α)

1. Bei α = 0° ist auch tan α = 0.
2. Bei α = 30° ist tan α = 0,577.
3. Bei α = 60° ist tan α = 1,732.
4. Bei α = 90° ist tan α nicht definierbar.
5. Bei α = 120° ist tan α = -1,732 und somit im negativen Bereich.
6. Bei α = 150° ist tan α = -0,577.
7. Bei α = 180° ist tan α = 0.
8. Bei α = 210° ist tan α = 0,577.
9. Bei α = 240° ist tan α = 1,732.
10. Bei α = 270° ist tan α nicht definierbar.
11. Bei α = 300° ist tan α = -1,732.
12. Bei α = 330° ist tan α = -0,577.
13. Bei α = 360° ist tan α wieder wie bei 0° und somit 0.
14. Der Verlauf der Tangenskurve.
15. Übersicht der Verläufe von Sinus, Kosinus und Tangens.

Übersicht über den Verlauf der Winkelfunktionen

Stellt man Sinus, Kosinus und Tangens in einer Übersicht und vergleicht sie miteinander, kann man sehen, wie unterschiedlich die Winkelfunktionen verlaufen. Die Verlaufsformen von Sinus und Kosinus ähneln sich zwar, beginnen jedoch mit unterschiedlichen Werten. Sinus beginnt mit 0, Kosinus dagegen mit 1. Tangens verhält sich ganz anders. Die Kurve geht steil nach oben und ist bei 90° und 180° nicht mehr definierbar. Das Pendant zu Tangens heißt Kotangens, wird jedoch nicht unbedingt benötigt. Daher betrachtet man bei den Winkelfunktionen meistens Sinus, Kosinus und Tangens.