Gleichsetzungsverfahren bei linearen Gleichungssystemen
Es gibt verschiedene Verfahren, um die Lösungsmenge für ein lineares Gleichungssystem zu lösen. Dazu gehört unter anderem das Gleichsetzungsverfahren. Die Vorgehensweise ist dabei wie folgt:
- Zunächst wählt man eine Variable aus, auf die beide Gleichungen umgestellt werden sollen.
- Beide Gleichungen des Gleichungssystems werden auf die ausgewählte Variable umgestellt.
- Beide Gleichungen werden nach der Umstellung gleichgesetzt und eine neue Gleichung entsteht.
- Dadurch entfällt die Variable, auf die man beide Gleichungen umgestellt hatte.
- Danach kann man die Gleichung auf die übrig gebliebene Variable umstellen.
Nachfolgend eine genaue Erläuterung in der Bildergalerie.
Zweites Beispiel für das Gleichsetzungsverfahren
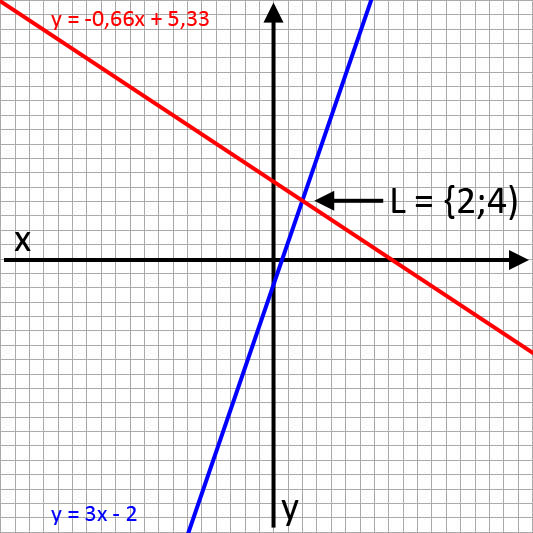
Grafische Lösung des Gleichungssystems
Man kann auf die Schnelle grafisch überprüfen, ob das Ergebnis des Additionsverfahrens richtig ist. Hierfür stellt man zuerst beide Gleichungen auf y um. Das Ergebnis ist:
y = 3x - 2
y = -0,66x + 5,33
Zeichnet man die beiden Geraden im kartesischen Koordinatensystem, erhält man exakt die berechnete Lösung. Der Schnittpunkt liegt bei 2 (X-Achse) und 4 (Y-Achse).