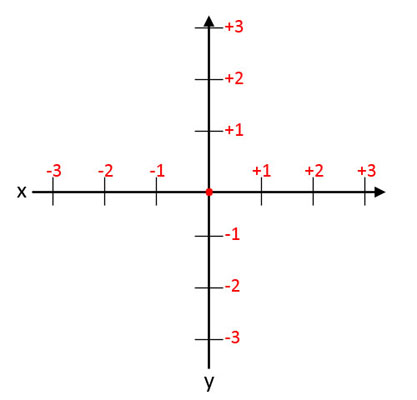
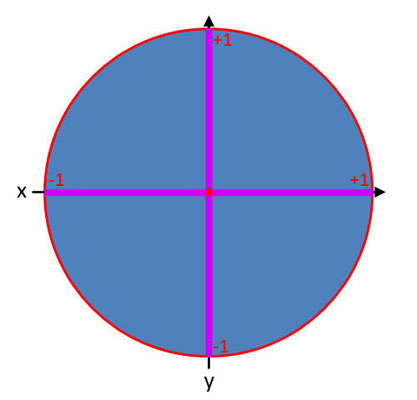
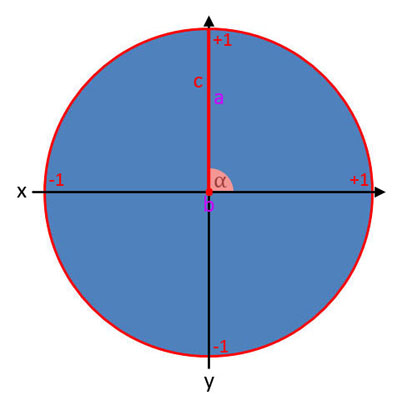
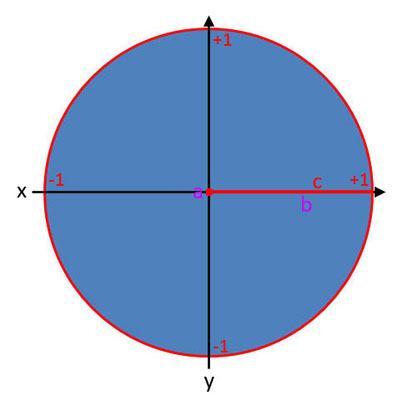
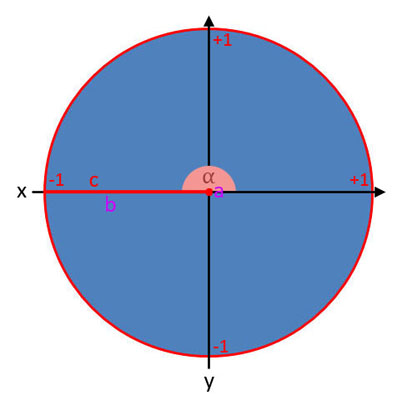
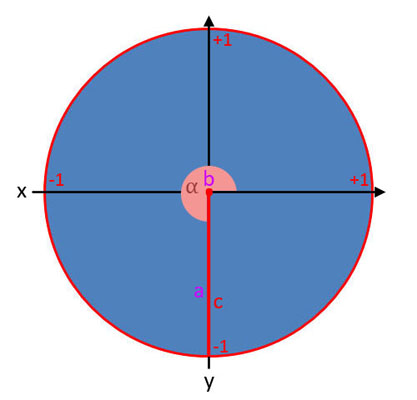
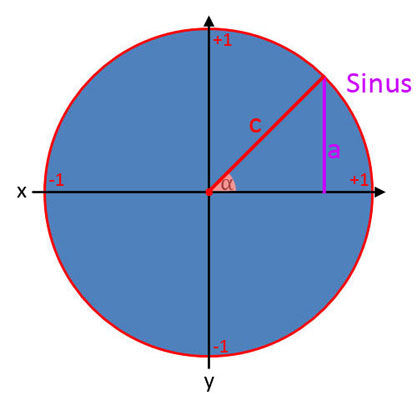
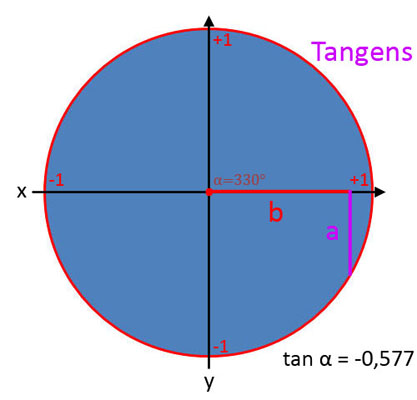
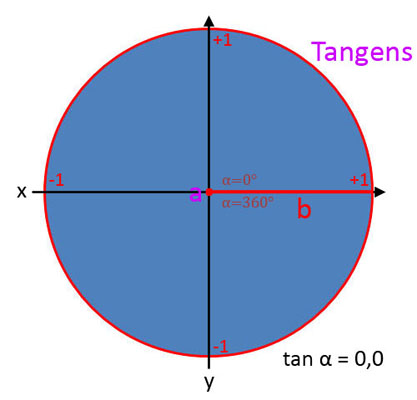
Darstellung der Winkelfunktionen im Einheitskreis
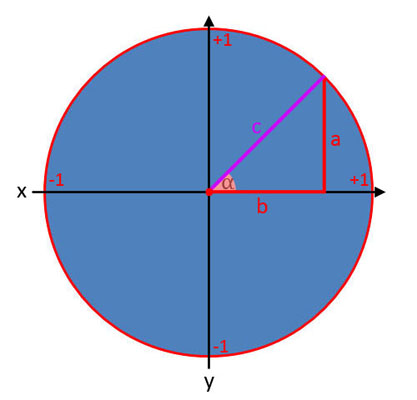
Ein rechtwinkliges Dreieck wird durch die Punkte A, B und C gebildet, wobei der rechte Winkel (90°) beim Punkt C liegt. Der Winkel Alpha liegt beim Punkt A, der Winkel Beta beim Punkt B. Die Seiten werden jeweils in Kleinbuchstaben so benannt, wie sie den Punkten A, B und C gegenüber liegen. Das bedeutet, die Seite, die gegenüber von Punkt C liegt, wird c benannt. Die gegenüber dem Punkt A liegende Seite wird a benannt, die gegenüber dem Punkt B liegende Seite b. Alle drei Winkel ergeben zusammen stets 180°. Das bedeutet, dadurch dass die Größe des rechten Winkels bekannt ist (90°), hat man die Größe von den beiden anderen Winkeln, sobald eine bekannt ist. Wenn z.B. β 70° ist, dann ist α 20° (180 - 90 - 70 = 20).
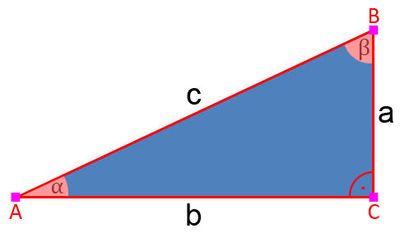
Die Seiten a, b und c hat man benannt und sie werden in Formeln wie folgt benutzt:
- Die längste Seite ist immer c und wird Hypotenuse genannt.
- Die Seite a ist die gegenüber vom Winkel α liegende Seite und wird daher Gegenkathete genannt.
- Die Seite b ist die am Winkel α anliegende Seite und wird daher Ankathete genannt.
Der Kern der Winkelfunktionen ist, dass man durch die Angabe einer Seitenlänge und des Winkels α alle übrigen Seitenlängen berechnen kann, da sie in einem Verhältnis zueinander stehen. Warum das so ist, wird durch den Einheitskreis im kartesischen Koordinatensystem verdeutlicht.
Bezeichnung der Seitenverhältnisse mit Sinus, Kosinus und Tangens in der Trigonometrie
Durch die Darstellung im Einheitskreis wird deutlich, dass die Seitenlängen a, b und c, abhängig vom Winkel α, in einem direkten Verhältnis zueinander stehen und daher mathematisch berechnet werden können. Hierfür hat man Gleichungen entwickelt und das Verhältnis der Seiten zueinander wurden wie folgt benannt:
- Sinus (sin): Ist das Verhältnis der Gegenkathete zur Hypotenuse.
- Kosinus (cos): Ist das Verhältnis der Ankathete zur Hypotenuse.
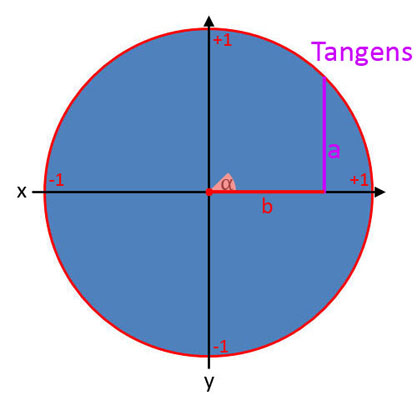
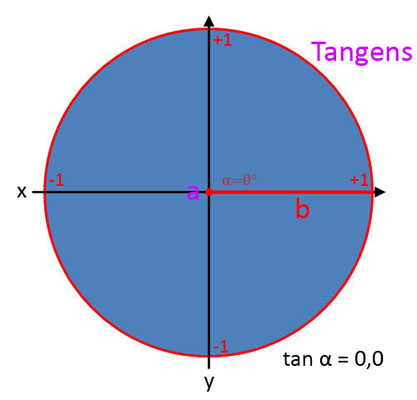
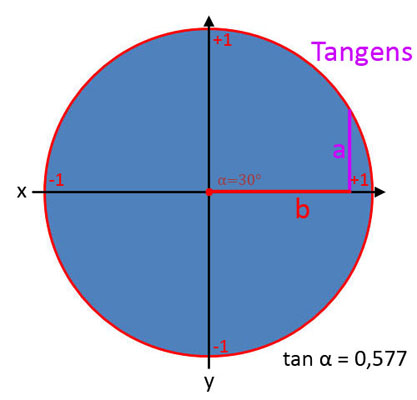
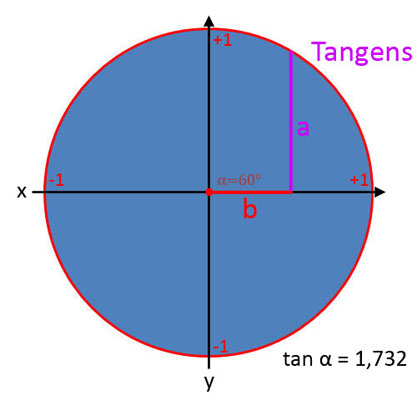
- Tangens (tan): Ist das Verhältnis der Gegenkathete zur Ankathete.
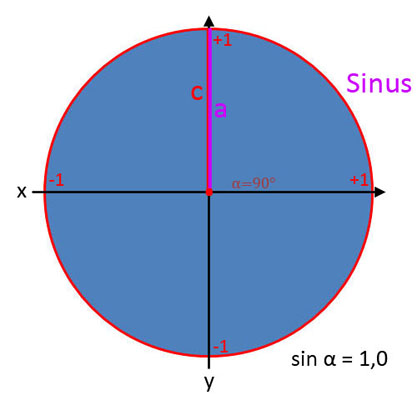
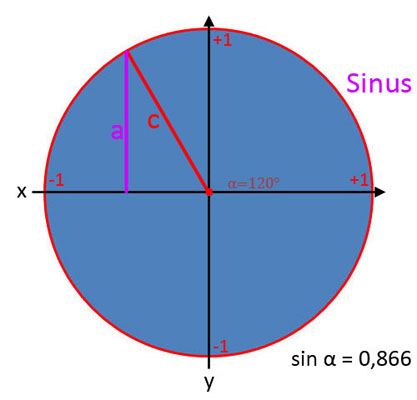
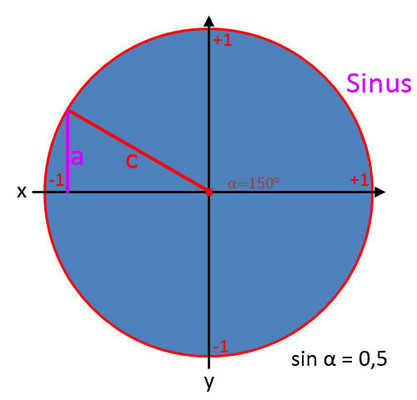
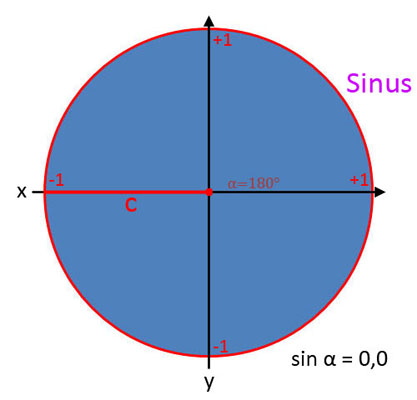
Um zu verdeutlichen, dass das Verhältnis von sin, cos und tan jeweils vom Winkel α abhängt, wird in Formeln das Zeichen α angehängt. Daher wird in Formeln für die Angabe des Verhältnisses sin α, cos α und tan α benutzt. Was genau sin α, cos α und tan α in der Trigonometrie bedeuten, wird in den nachfolgenden Bildergalerien gezeigt.
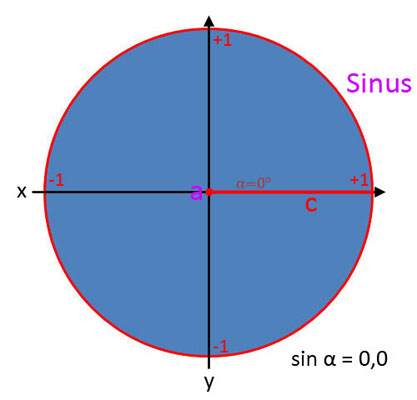
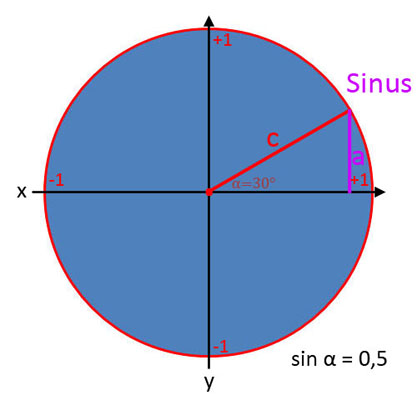
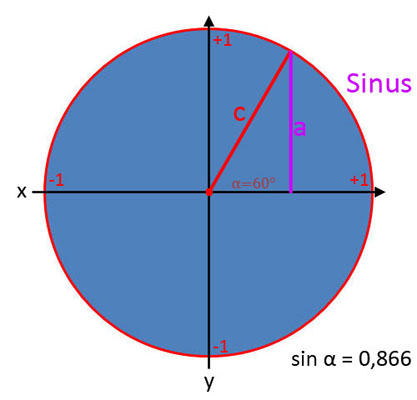
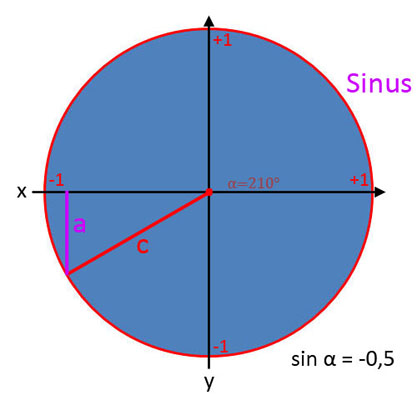
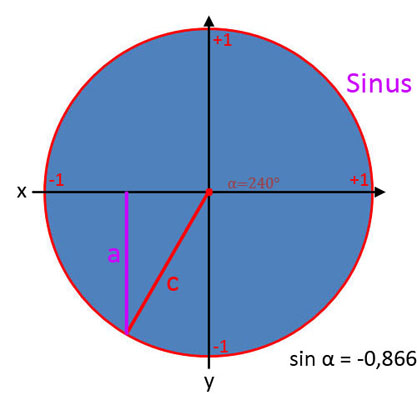
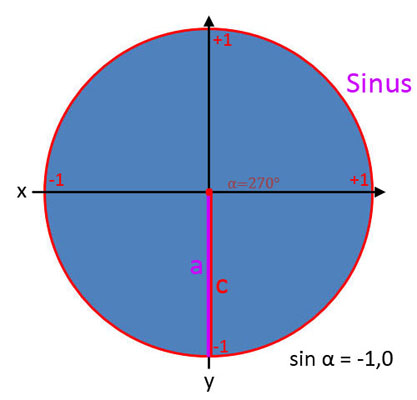
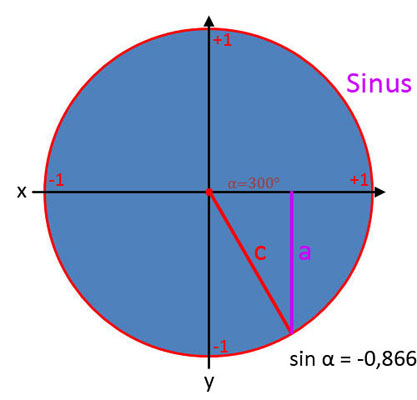
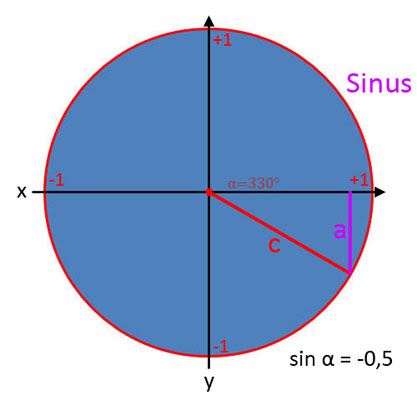
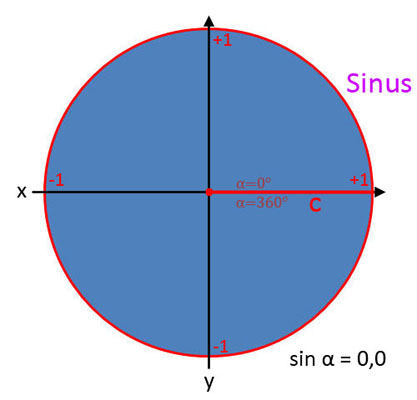
Sinus (sin α)
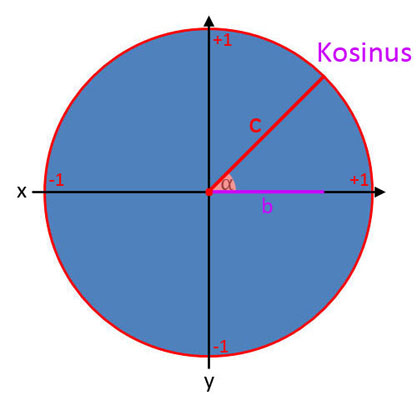
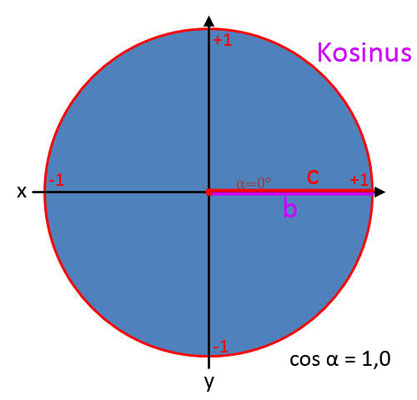
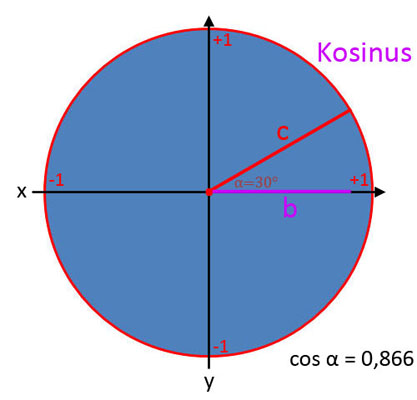
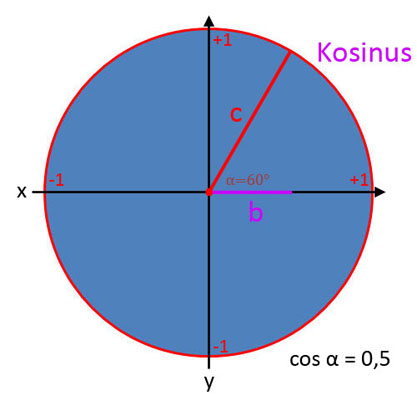
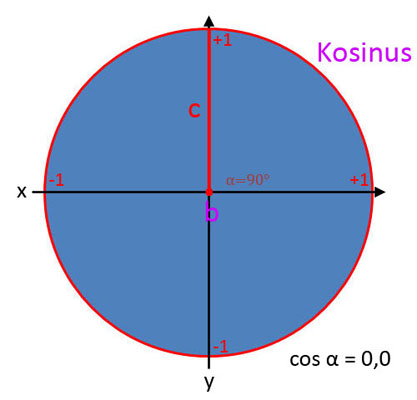
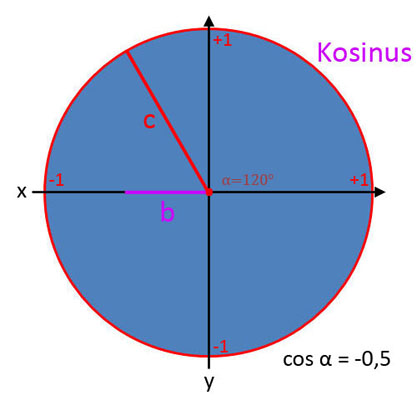
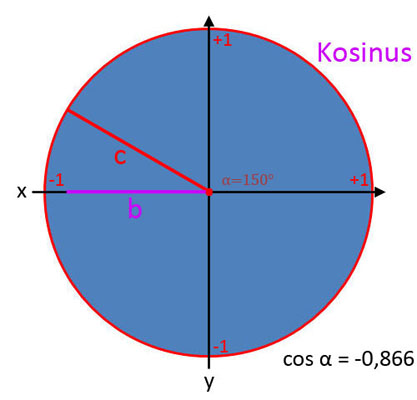
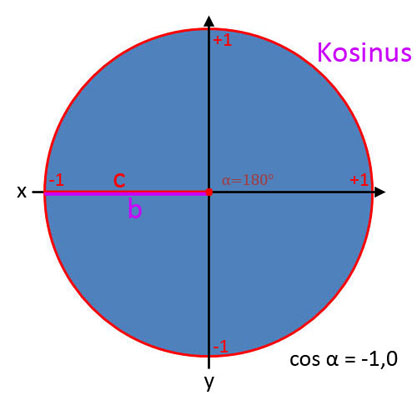
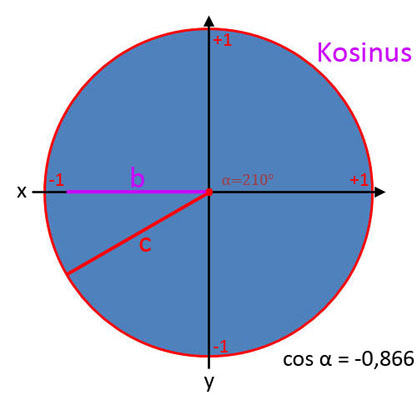
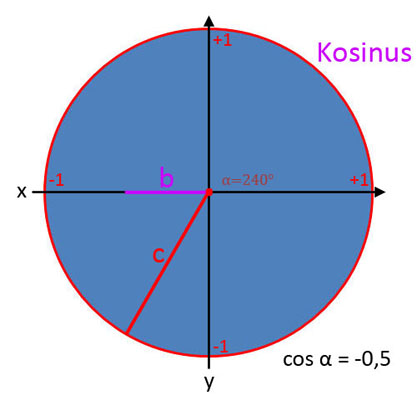
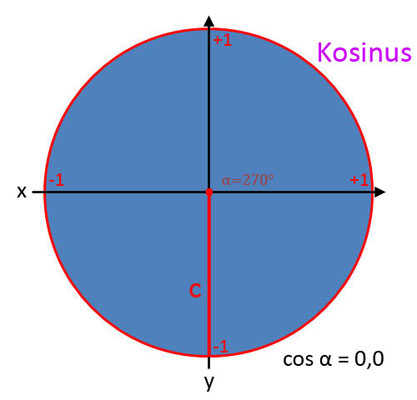
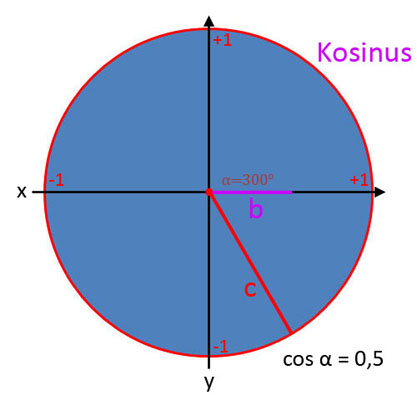
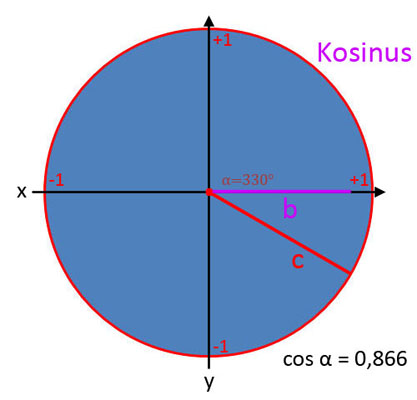
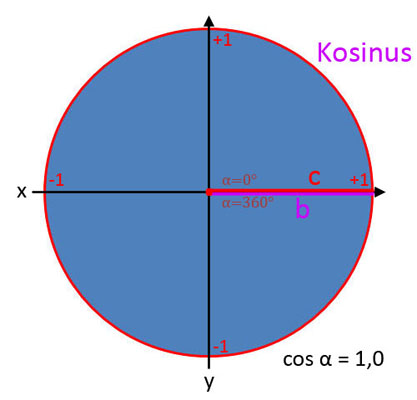
Kosinus (cos α)
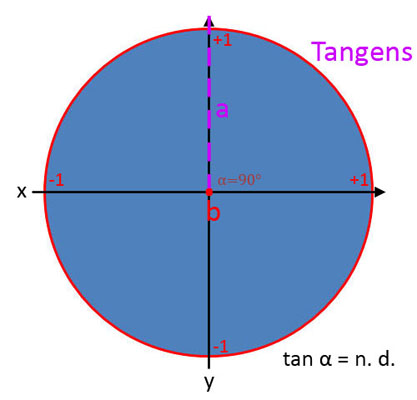
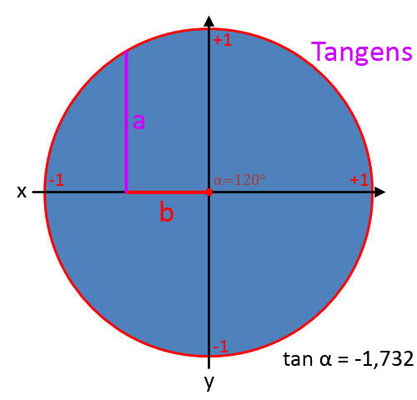
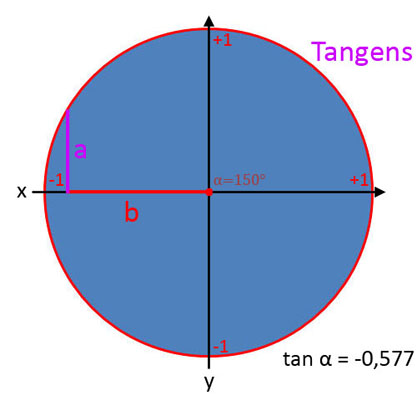
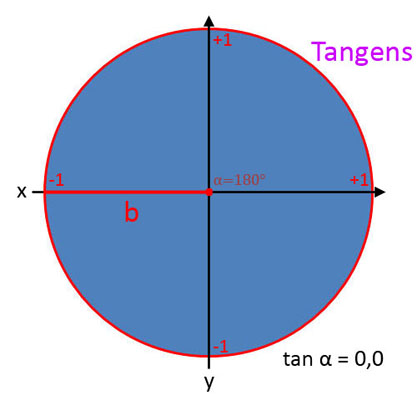
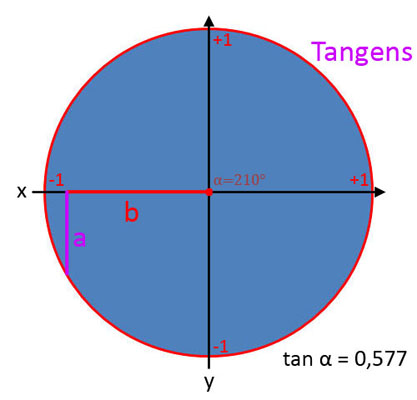
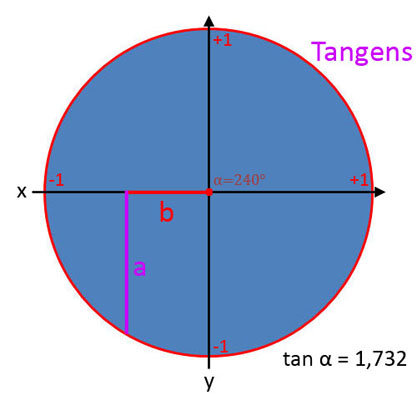
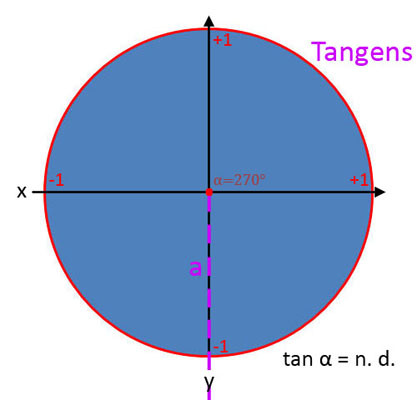
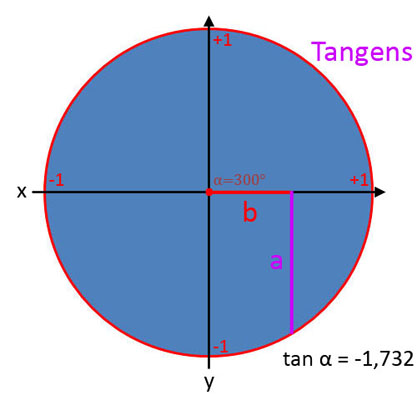
Tangens (tan α)
Zusammenfassen der Winkelfunktionen und Formeln bilden
Zusammenfassend kann man sagen, dass man abhängig vom Winkel α, mit Sinus und Kosinus berechnen kann, wie lang die Seite a (Gegenkathete) und b (Ankathete) im Verhältnis zu c (Hypotenuse) ist. Mit Tangens kann man bestimmen, wie lang die Seite a im Verhältnis zu b ist. Daraus lassen sich folgende Formeln ableiten:
- Gegenkathete = Hypotenuse · sin α
- Ankathete = Hypotenuse · cos α
- Gegenkathete = Ankathete · tan α
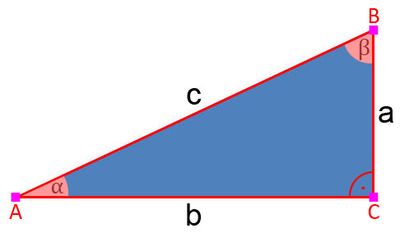
Bezogen auf das abgebildete Dreieck bedeutet das:
- a = c · sin α
- b = c · cos α
- a = b · tan α
Wenn man die Hypotenuse berechnen will, muss man, je nachdem welche Seite bekannt ist, eine von den ersten beiden Formeln umstellen. Daraus bildet man folgende Formeln:
- Hypotenuse = Gegenkathete : sin α
- Hypotenuse = Gegenkathete : cos α
Bezogen auf das abgebildete Dreieck bedeutet das:
- c = a : sin α
- c = a : cos α
Ermitteln von sin α, cos α und tan α
In den Bildergalerien wurde z.B. gezeigt, dass sin α bei einem Winkel von α = 30° einen Wert von 0,5 hat. Eine gute Frage ist, wie kommt man denn nun auf den Wert? Hierbei gibt es mehrere Möglichkeiten. Wenn z.B. zwei Seiten bekannt sind, dann braucht man nur die Formeln umstellen. Daraus resultieren folgende Gleichungen:
- sin α = Gegenkathete : Hypotenuse
- cos α = Ankathete : Hypotenuse
- tan α = Gegenkathete : Ankathete
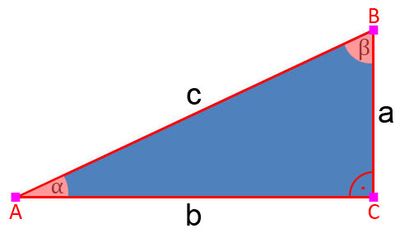
Bezogen auf das abgebildete Dreieck bedeutet das:
- sin α = a : c
- cos α = b : c
- tan α = a : b
Was macht man aber, wenn nur eine Seite und der Winkel α bekannt ist? Der Verlauf der Winkelfunktionen kann zwar grafisch dargestellt werden, zum Ablesen von konkreten Werten ist das jedoch zu ungenau. Früher wurden häufig Tabellenbücher benutzt und die Werte daraus abgelesen. Es sind schließlich konstante Werte. Beispielsweise ist sin α bei einem Winkel von α = 30° immer 0,5. Es gibt natürlich auch sehr aufwendige Methoden, sin α, cos α und tan α zu berechnen. Allerdings ist das heutzutage nicht mehr nötig. Tippt man in den Taschenrechner den Winkel ein und drückt danach die SIN-, COS- oder TAN-Taste, dann erhält man den Wert.
Umwandeln von sin α, cos a oder tan α und ermitteln des Winkels α
Zunächst einmal muss man sich immer verdeutlichen, dass sin α, cos α oder tan α nicht den Wert des Winkels α darstellen. Wenn z.B. der Winkel α = 30° ist, dann ist sin α = 0,5 und stellt nur das Verhältnis der Gegenkathete zur Hypotenuse dar. Wenn es jedoch möglich ist, nur durch die Angabe des Winkels α den Wert von sin α, cos α oder tan α zu ermitteln, dann muss es ja auch einen Weg rückwärts geben. Nämlich, den Winkel durch die Angabe von sin α, cos α oder tan α zu ermitteln. Schließlich erhält man z.B. durch die Gleichung sin α = Gegenkathete : Hypotenuse lediglich den Wert sin α und nicht den Wert vom Winkel α. Häufig möchte man jedoch, wenn zwei Seiten bekannt sind, den dazugehörigen Winkel ermitteln.
Auch hier gilt, dass man früher häufig Tabellenbücher benutzte. Genauso wie man die Werte von sin α, cos α und tan α auslesen konnte, konnte man durch die dazugehörigen Werte den Winkel α ermitteln. Man kann auch den Winkel α durch aufwendige Berechnungen ermitteln. Aber das ist heutzutage nicht mehr notwendig. Genauso wie man über den Taschenrechner sin α, cos α und tan α ermitteln kann, kann man den Winkel α ermitteln. Häufige Vorgehensweise hier: Man tippt den Wert von sin α, cos α oder tan α ein, drückt die SHIFT-Taste und drückt danach, je nachdem was man eingegeben hat, die SIN-, COS- oder TAN-Taste und man erhält den Wert des Winkels α.
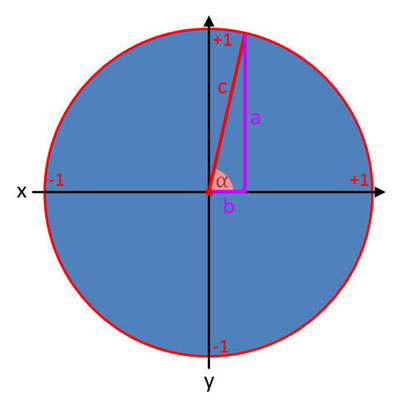
Anwenden der Winkelfunktionen auf den Winkel β
Bisher hat man lediglich den Winkel α berücksichtigt. Dadurch, dass die Winkelsumme eines Dreiecks immer 180° ist, der Wert des rechten Winkels bekannt ist (90°), hat man automatisch den Wert von β, wenn man den Wert von α hat (180 - 90 - α = β). Bei den Winkelfunktionen kann auch mit dem Wert von β gearbeitet werden. Es ist egal, ob der Winkel stumpf oder spitz ist. Die Formeln bleiben wie gehabt.
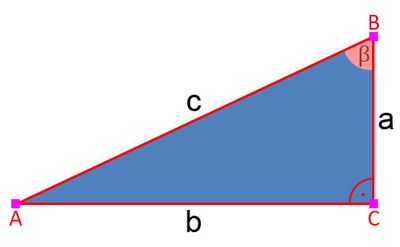
Der einzige Unterschied ist, dass in den Formeln die Seiten a und b vertauscht werden. Denn, wenn man statt mit α mit dem Winkel β arbeitet, dann ist die am Winkel anliegende Seite nicht mehr b, sondern a, die Seite, die dem Winkel gegenüberliegt ist b. Die bisher benannten Formeln müssen daher bei der Berechnung mit dem Winkel β wie folgt umgewandelt werden:
- b = c · sin β (Gegenkathete = Hypotenuse · sin β)
- a = c · cos β (Ankathete = Hypotenuse · cos β)
- b = a · tan β (Gegenkathete = Ankathete · tan β)
- c = b : sin β (Hypotenuse = Gegenkathete : sin β)
- c = b : cos β (Hypotenuse = Gegenkathete : cos β)
- sin β = b : c (sin β = Gegenkathete : Hypotenuse)
- cos β = a : c (cos β = Ankathete : Hypotenuse)
- tan β = b : a (tan β = Gegenkathete : Ankathete)