Bruchgleichungen lösen

Beim Umstellen von Gleichungen kommt es häufig vor, dass auf einer oder beiden Seiten ein Bruch vorhanden ist. Das stellt per Definition noch keine Bruchgleichung dar. Eine Gleichung ist dann eine Bruchgleichung, wenn es mindestens einen Bruchterm enthält. Ein Bruchterm ist definiert als ein Bruch, der im Nenner eine Variable enthält.

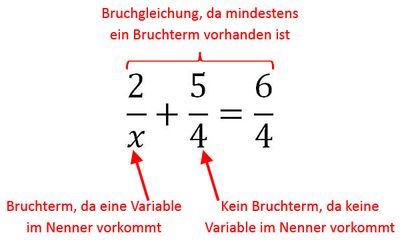
Ob man nun eine Variable im Nenner hat oder nicht, spielt jedoch bei der Umstellungen keine Rolle. Die mathematischen Schritte zum Vereinfachen und Lösen von Bruchgleichungen sind dieselben wie beim Lösen von Gleichungen ohne Bruchtermen und sollten daher keine Rolle spielen. Um Bruchgleichungen lösen zu können, sollten Kenntnisse im Bereich Bruchrechnen und Umstellen von Formeln vorhanden sein.

Lösen von Bruchgleichungen mit einem Bruch

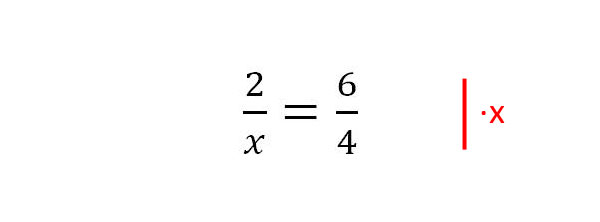
1. Die Formel soll nach x umgestellt werden. Zuerst wird das x im Nenner entfernt. Da ein Bruchstrich eine Division darstellt, entfernt man den Nenner mit einer Multiplikation.
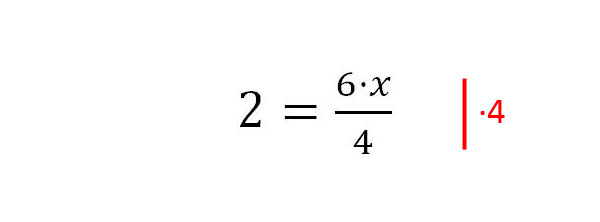
2. Im nächsten Schritt wird die 4 im Nenner entfernt. Auch wieder durch Multiplikation.
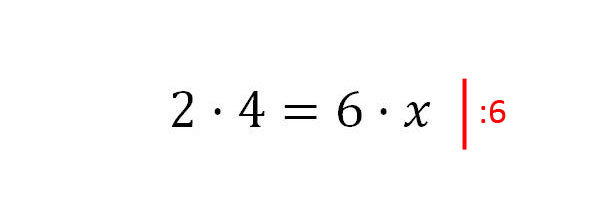
3. Nun wird die 6 entfernt, damit auf x umgestellt wird.
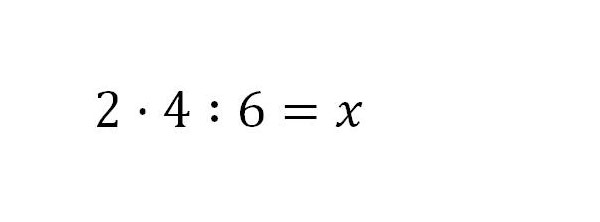
4. Danach kann x berechnet werden.
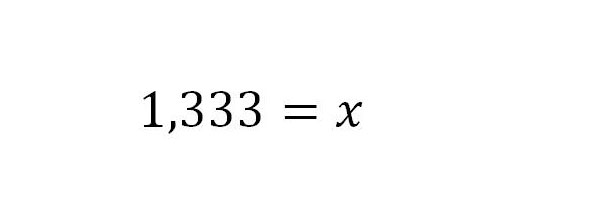
5. Das Ergebnis ist 1,333 für x.
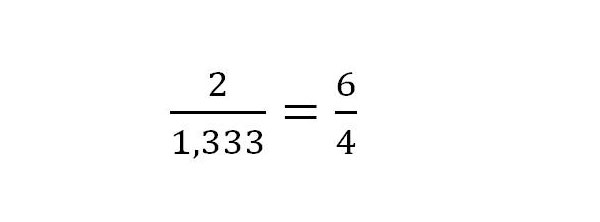
6. Als Gegenprobe setzt man das Ergebnis in die Ursprungsgleichung anstelle von x ein.
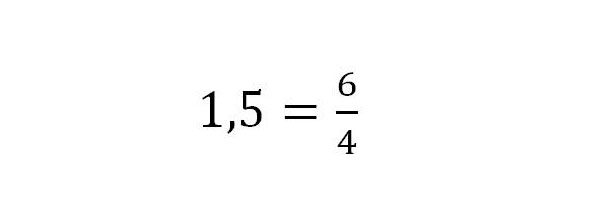
7. Die Berechnung ergibt 1,5. Auf der rechten Seite ist 6 : 4 ebenfalls 1,5. Das Ergebnis stimmt also.

Bruchgleichungen mit 2 Brüchen lösen

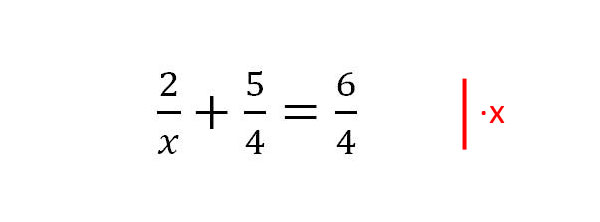
1. Bei dieser Gleichung hat man auf der linken Seite 2 Brüche. Die Gleichung soll auf x umgestellt werden. Zunächst wird das x mit · x entfernt.
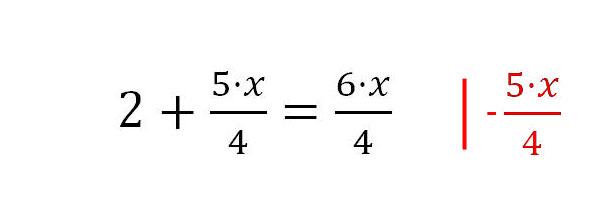
2. Dabei muss man aufpassen. Denn, nicht nur der Bruch auf der rechten Seite wird mit · x erweitert, sondern auch der Bruch 5/4 auf der linken Seite. Im nächsten Schritt wird der Bruch mit dem x auf die rechte Seite geholt.
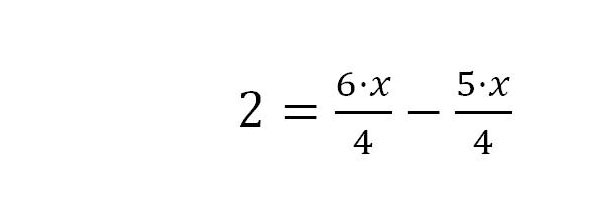
3. Der rechte Term kann berechnet werden.
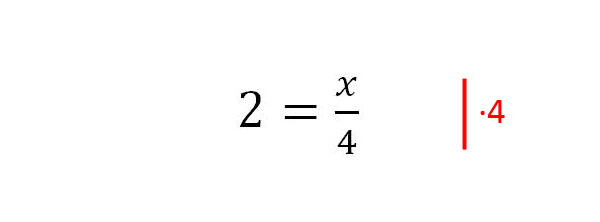
4. Übrig bleibt x/4. Danach wird mit · 4 auf x umgestellt.
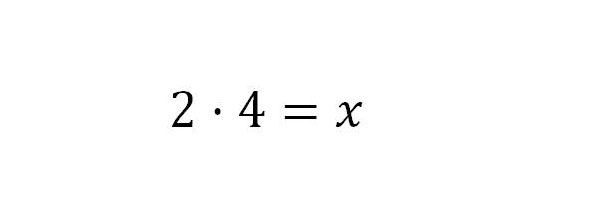
5. Auf der rechten Seite ist x nun allein und die linke Seite wird berechnet.
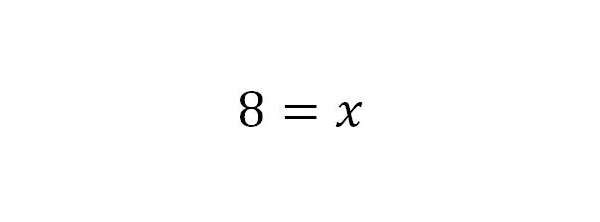
6. Das Ergebnis ist 8 = x.
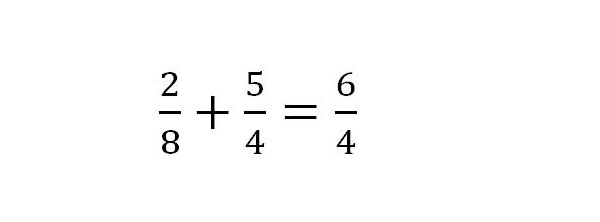
7. Als Gegenprobe wird das Ergebnis in die Ursprungsgleichung anstelle von x eingesetzt. Um den linken Term zu berechnen, bringt man alles auf einen Nenner.
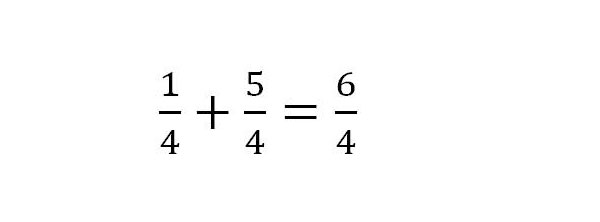
8. 2/8 sind 1/4. Der linke Term wird nun berechnet und das Ergebnis stimmt.

Bruchgleichungen mit mehreren Variablen und negativen Vorzeichen

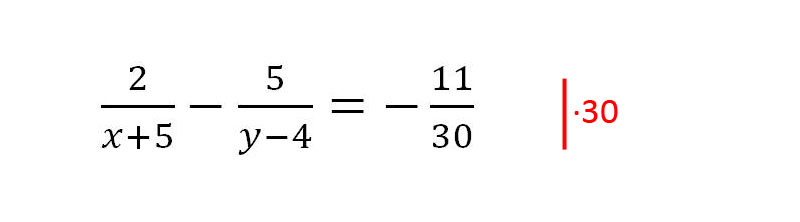
1. Diesmal hat die Bruchgleichung mehrere Variablen (x und y) und negative Vorzeichen. Die Gleichung soll nach x aufgelöst werden. Im ersten Schritt wird die 30 vom rechten Bruch entfernt.
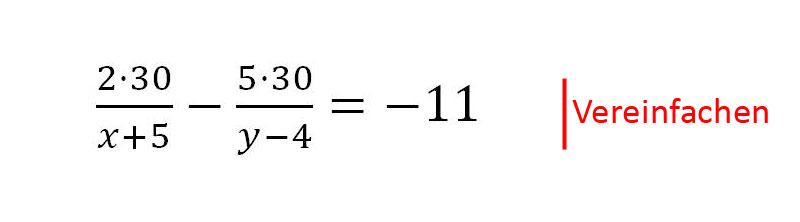
2. Es wird vereinfacht.
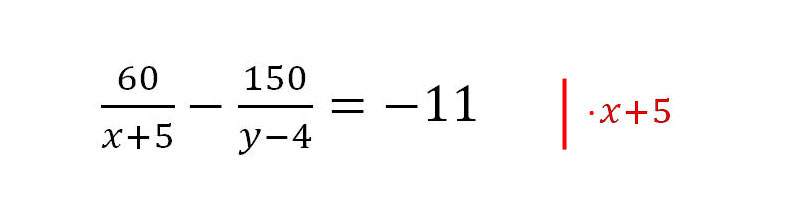
3. Als nächstes wird x + 5 entfernt.
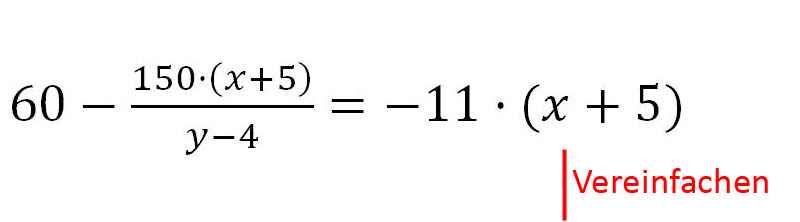
4. Es wird wieder vereinfacht.
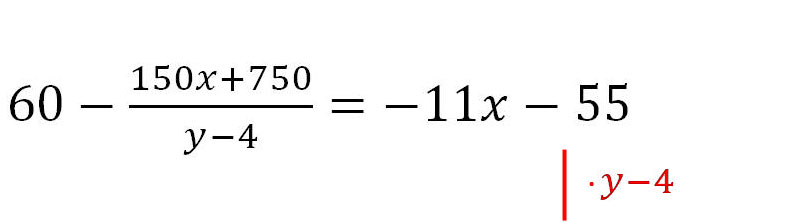
5. Nun wird y - 4 entfernt.
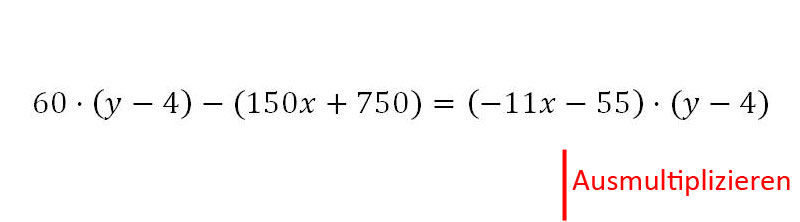
6. Hierbei muss man aufpassen. Befindet sich vor dem Bruchstrich ein Minuszeichen, muss der Zähler eingeklammert werden. Alle Brüche sind entfernt. Es wird ausmultipliziert.
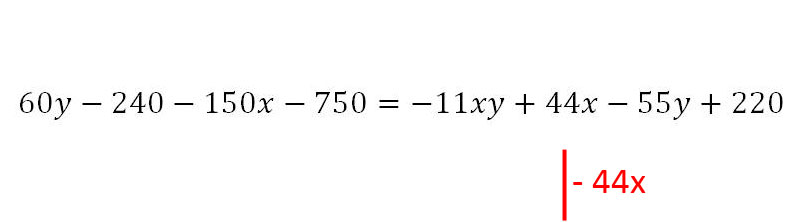
7. Danach wird begonnen, alles was mit x zu tun hat, auf die linke Seite zu bringen und alles andere auf die rechte Seite. Wir beginnen mit + 44x.
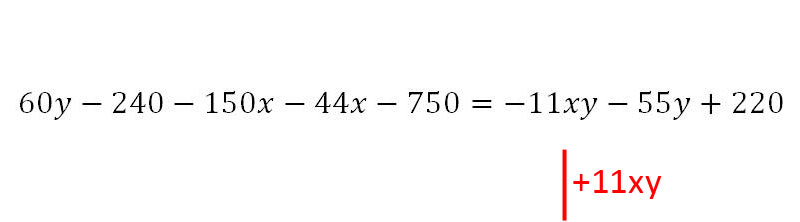
8. Als nächstes wird - 11xy auf die linke Seite gebracht.
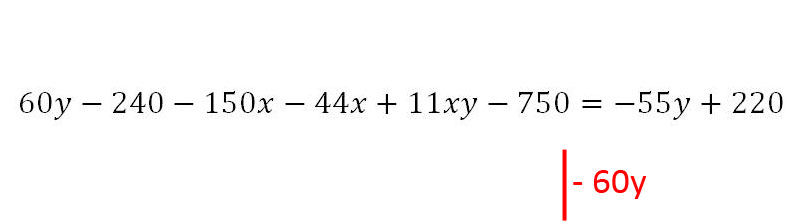
9. Nun wird damit begonnen, alles was kein x enthält, auf die rechte Seite zu bringen. Der Anfang wird mit 60y gemacht.
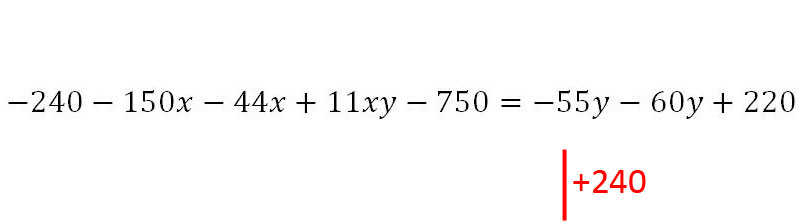
10. Als nächstes folgt - 240.
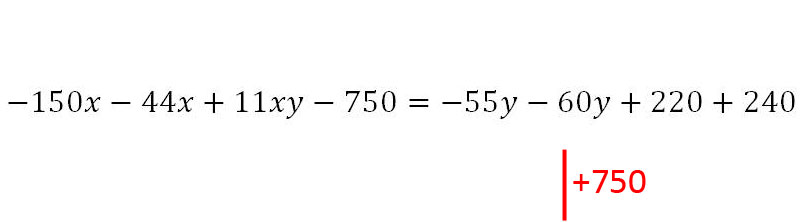
11. Danach - 750.
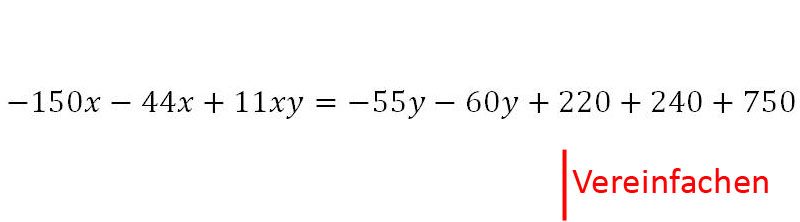
12. Die Gleichung kann jetzt vereinfacht werden.
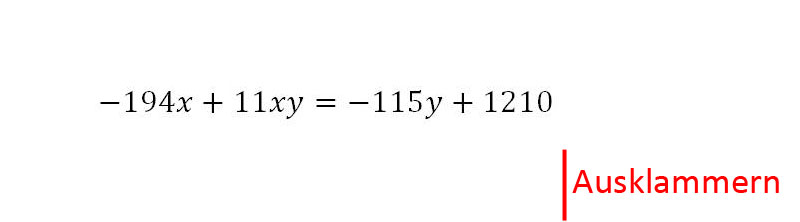
13. Auf der linken Seite muss x gelöst werden. Das wird durch Ausklammern erreicht.
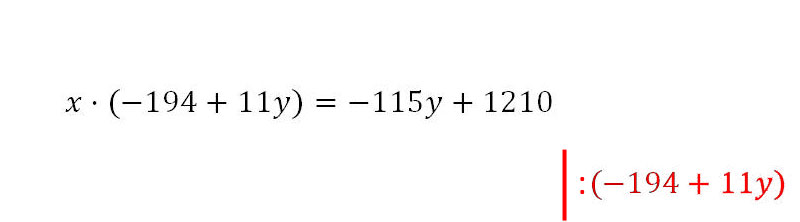
14. Nun kann (-194 + 11y) auf die rechte Seite gebracht werden.
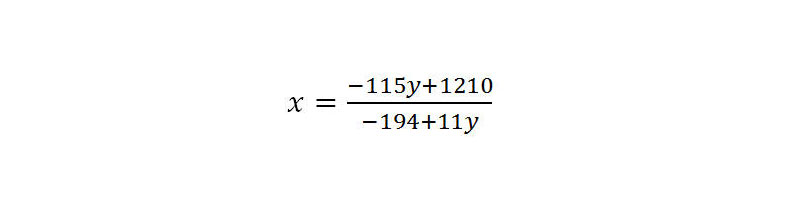
15. Die Gleichung ist umgestellt.